Going further with Point Sprite Sphere Impostors

This picked up where the last project left off. Honestly, it's hard to even recognize it as the same project, but there are actually very few material changes between the two - very similar projects, and in fact this one stripped out a lot of code from the last. One of the big things was the move to a deferred pipeline, to enable several things that I previously had not realized were possible. I've now realized that some of the motivation to write SoftRast was actually misguided, and much of what I have done with that project is totally possible with the OpenGL API. That doesn't negate it as having been a useful exercise, and potentially being a useful utility in the future. Before implementing pieces of this project, I just wasn't aware of how these things were done using the hardware accelerated OpenGL API. You can render to all sorts of different data types, using color attachments to framebuffer objects - it's a very powerful feature, which opens a lot of doors.
Deferred Pipeline
A deferred pipeline is a method of taking the raster output and writing the result to one or more textures, which are then used later for shading. This set of textures is broadly referred to as the Gbuffer. This is in contrast with forward rendering, where you use the raster result to do your shading immediately in the fragment shader. One of the major benefits of this approach is that shading complexity becomes more directly correlated with the resolution of the screen, rather than the number of primitives. This can enable the use of a large number of lights, for example, this implementation was able to handle over a thousand blinn-phong lights and maintain realtime framerates.
There is a significant memory bandwidth cost associated with making the rasterizer write these results to the color attachments, and this part does in fact scale with the primitive count, so you do have to be aware that it is not free. The cool thing is, as I mentioned before, each color attachment can have a different data type, number of channels, etc. Depending on what you want to represent, you can write unsigned integers, half precision floats, single precision floats, and more. I used three color attachments and a depth attachment: a GL_RGBA16F buffer for worldspace position, a GL_RGBA16F buffer for worldspace normals, and a GL_R32UI buffer for an ID, basically what is called a visibility buffer. There is a significant amount of cool stuff that comes along with the visibility buffer - I will explain.
The raster pass renders out all the points at once - one draw call. Each vertex shader invocation has an ID value in gl_VertexID. I used this value to reference an SSBO which held positions and point sizes, which can be used with glEnable( GL_PROGRAM_POINT_SIZE ) / gl_PointSize to control the scaling of the point primitives as a vertex shader output. By writing also this gl_VertexID to the 32-bit unsigned integer buffer per pixel, I can uniquely identify which vertex shader invocation wrote to that pixel when computing the shading result, which one established the closest surface by passing the depth testing.
You might notice that I didn't mention an actual color value being written to any of these color attachments - there is a reason for that. Because I have this unique index for every pixel, I can reference the same SSBO data, and pull that color value for each sphere at shading time. This can easily be extended to handle material properties, etc, as well. Additionally, you could read from this buffer at the mouse location, to do picking for up to 4 billion unique points. The renderer scales to the tens- or hundreds-of-millions territory before becoming unreasonably slow, so that is more than sufficient precision to keep a unique ID for every primitive, and have bits left over to pass additional data in that channel.
Shading, Lighting, SSAO
Shading with a deferred pipeline involves running the rasterizer to create the render results, then using that in another pass, to compute the shading result. In this case, that is a compute shader that runs with two sets of these buffers, representing the result from this frame, and the frame previous. There is an additional output accumulator buffer, which holds state across multiple frames. This contributes to a couple of effects, which I will touch on in the next section on Temporal Resolve.

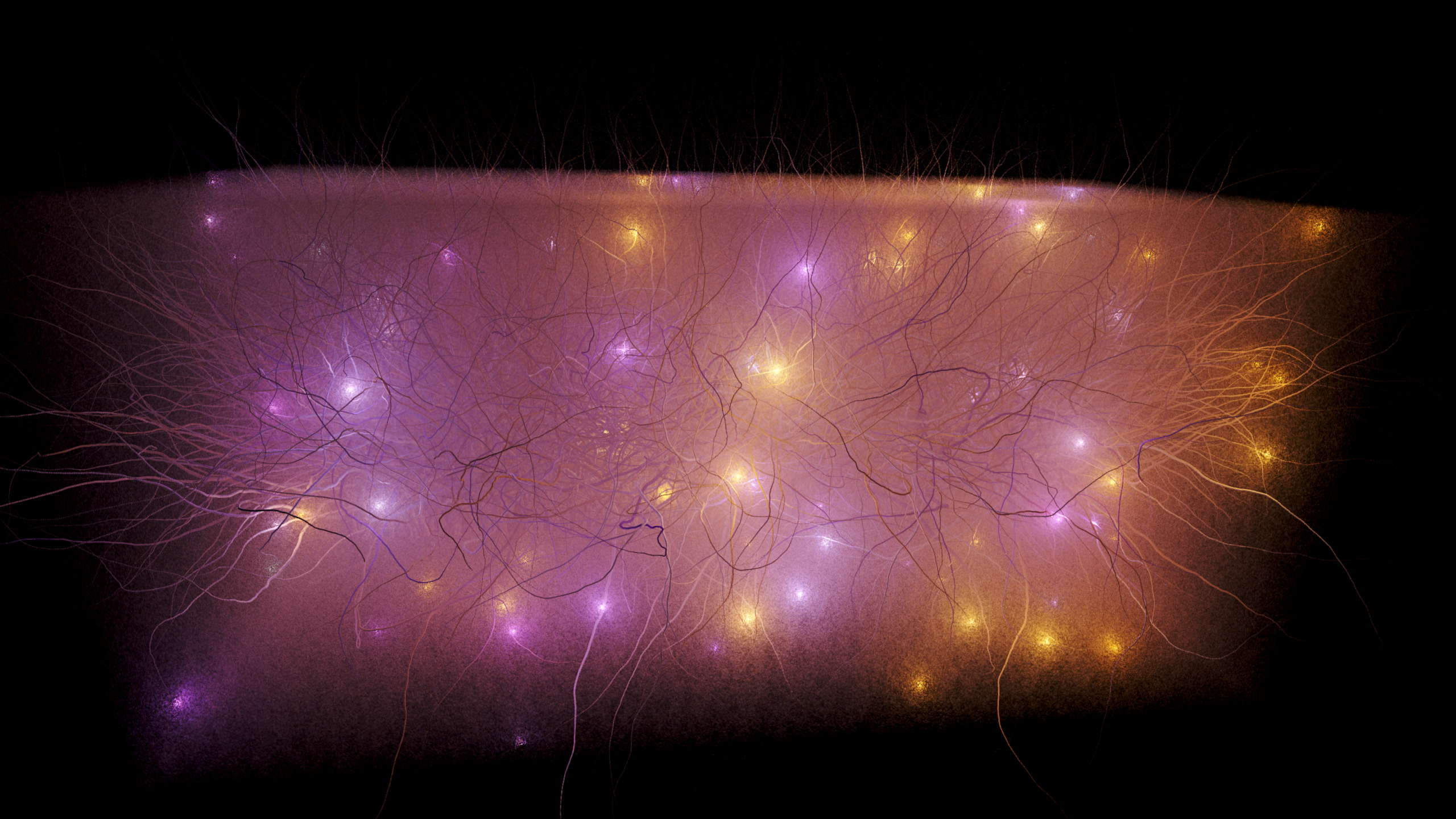
Iterating through the list of lights for every texel in the framebuffer, and calculating the contribution from each one, we get the final shading result. I used a sum of several lights, using the blinn-phong lighting model. I also calculate a screenspace ambient occlusion ( SSAO ) term, which darkens pixels based on how much light or shadow they would recieve based on information from nearby framebuffer texels. I referred to this implementation, by Reinder Nijhoff on Shadertoy. This is a cheap approximation based on samples taken in a spiral around each texel, instead of accumulating many samples of the light attenuation you would get from nearby geometry in e.g. a pathtracer.
Temporal Resolve
This folds right into the topic of how the data is managed and blended over time. This shading result is computed every frame, producing an output color for every texel. When that result is computed, it is blended with the previous state of the framebuffer at a ratio of 100:1, with a bias towards the existing state of the buffer. This leaves significant ghosting under movement - but I have found that it's an interesting way to model volumetric effects. As you blend the framebuffer result with the new render result, you can approximate the ground truth of what should be displayed.
I moved to an analytic representation of the spheres, as well - using the Pythagorean theorem, courtesy of Simon Green - this is in contrast to using a texture, with a limited amount of detail held in the data. By using the analytic model, I'm able to resolve it as well as floating point precision will allow. Using blue noise to offset the subpixel sample location, what's known as pixel stratified jitter, I'm able to resolve the outline over multiple frames, and get a good approximation of the normal, position, etc, of the sphere for each pixel. Moving from a texture to an analytic model has a couple benefits - instead of relying on a limited set of data in the texture, I can resolve this much higher fidelity outline, and it's also good for about a 30% speedup.
One of the things that I'm still not quite perfect on, is what is referred to as TAA. This is a complex topic, with a lot of moving parts. Basically, you are using what is referred to as reprojection of the previous frame's data, to align with the current frame's data, and using some thresholding logic in order to determine whether or not results can be reused. For example, if the distance changes a significant amount between frames, after correcting for movement, it's unlikely that we are looking at the same surface, and we probably want to reject the contribution from the previously accumulated result. I have experienced a result with a significant amount of noise, especially at the edges of the point sprite primitives, because of how the subpixel jitter affects the way that each pixel resolves.
It's been brought to my attention that often times, TAA uses a constant jitter value across every pixel in the entire viewport, where I've been applying a different jitter value for every pixel in the framebuffer. This means that I am basically evaluating a different position inside of each pixel each frame, eventually resolving a good approximation of "how much sphere actually sits behind the pixel". This uses the analytic model and rejects samples of the pixel which fall outside of the sphere's footprint, using an exact methodology, not relying on the limited quality of the data that exists in the texture. By getting these multiple samples, and blending over multiple frames, we get this progressive approximation of what the pixel data should represent.


You can see here the comparison between one frame's sample on the left, and the same view, resolved over many frames on the right.
Volumetrics
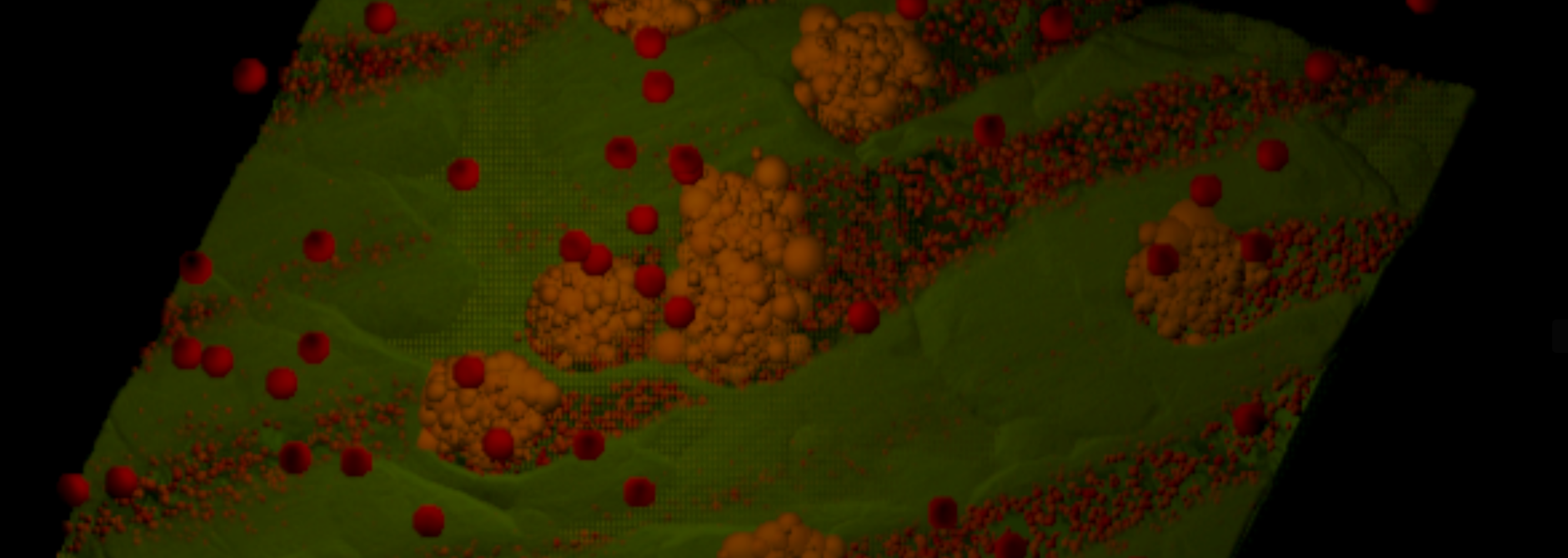
The points which are used to model the volumetrics move through space with a compute shader. That is, their positions are randomly jittered, and when they exit a certain volume, they reappear on the opposite side of that volume. Because their color contributions are considered the same as the rest of the points, their movement creates a distribution over time, a probability that they are either there or not there during any given frame.

Because their position is static during any given frame, they look the same as the rest of the static points - it is only their movement over time that creates this effect. Since they recieve lighting the exact same way as the rest of the points, the blinn-phong lighting emulates a primary scattering event for participating media in a volume. When it is blended over multiple frames, this ends up looking like this foggy, partially transparent volumetric effect. You can see the area of influence for each light, here. Again, nothing but a consequence of them passing through. I have been referring to this effect as Point Distribution Volumetrics.
Applications
Several different usages presented themselves once I started messing with this rendering method. I realized, if you can draw so many of these, you really can start to create smooth surfaces with the data. There is nothing that keeps you from placing them close enough together than you start to see continuous lines, close enough that you would not see any concavity between neighboring pixels. It's probable that you could calculate the required density, but I basically just experimented with what looked "good enough". You can see here, the first time I messed with straight line segments:

What it looks like with continuous curvature, extending the above to change the path between each placed point, following some sinusoidal paths, rather than continuing on some segmented path for several placements:

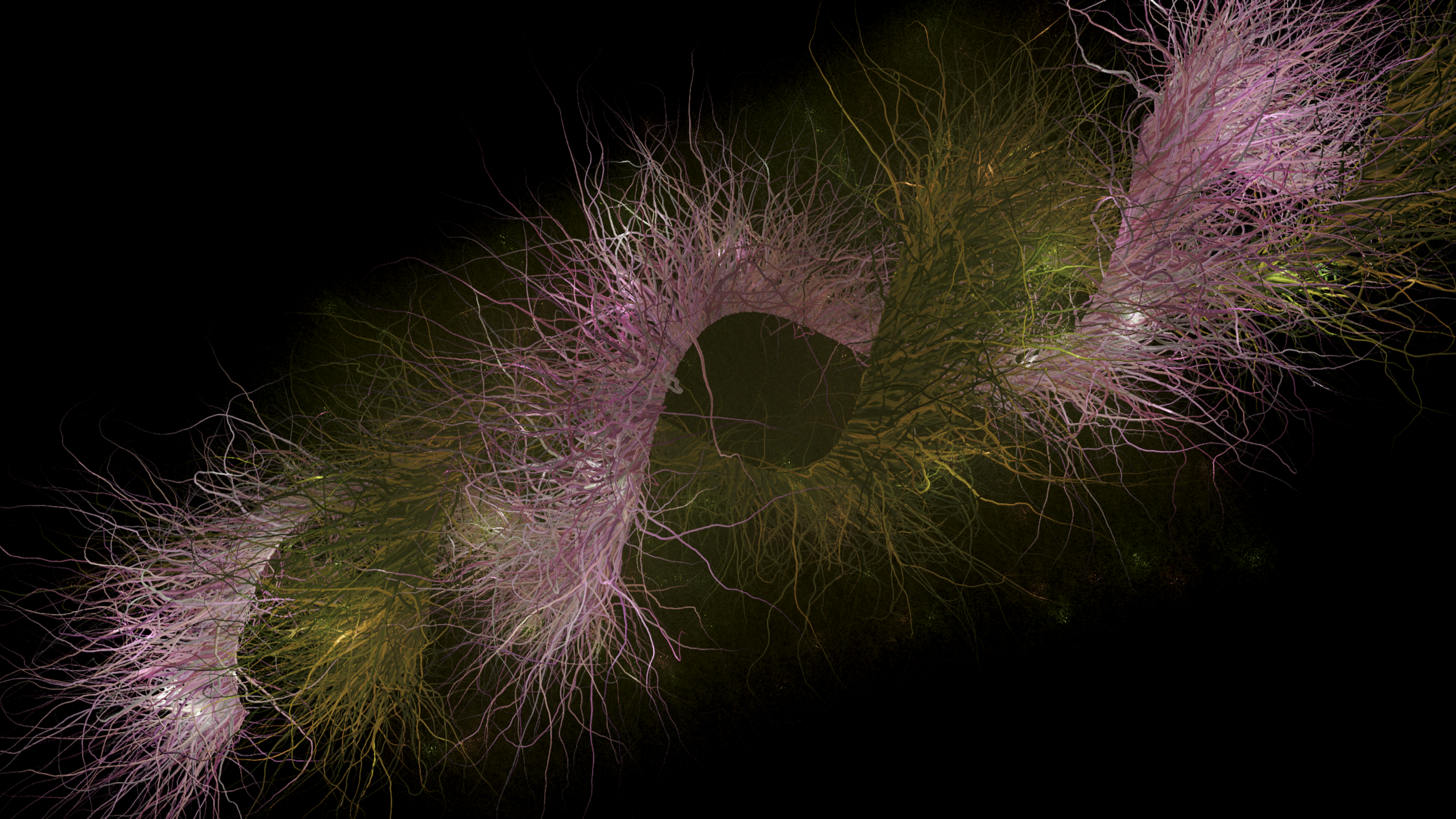
And a further experiment with this methodology, where point placement became a recursive process, with a certain chance to branch, at each step. By doing it this way, you start to resolve this very high quality hair rendering method that works in realtime. It does largely require that the geometry is static, in my implementation, but it might make sense if you did an offline process to resolve the image over multiple frames each time you updated the geometry.
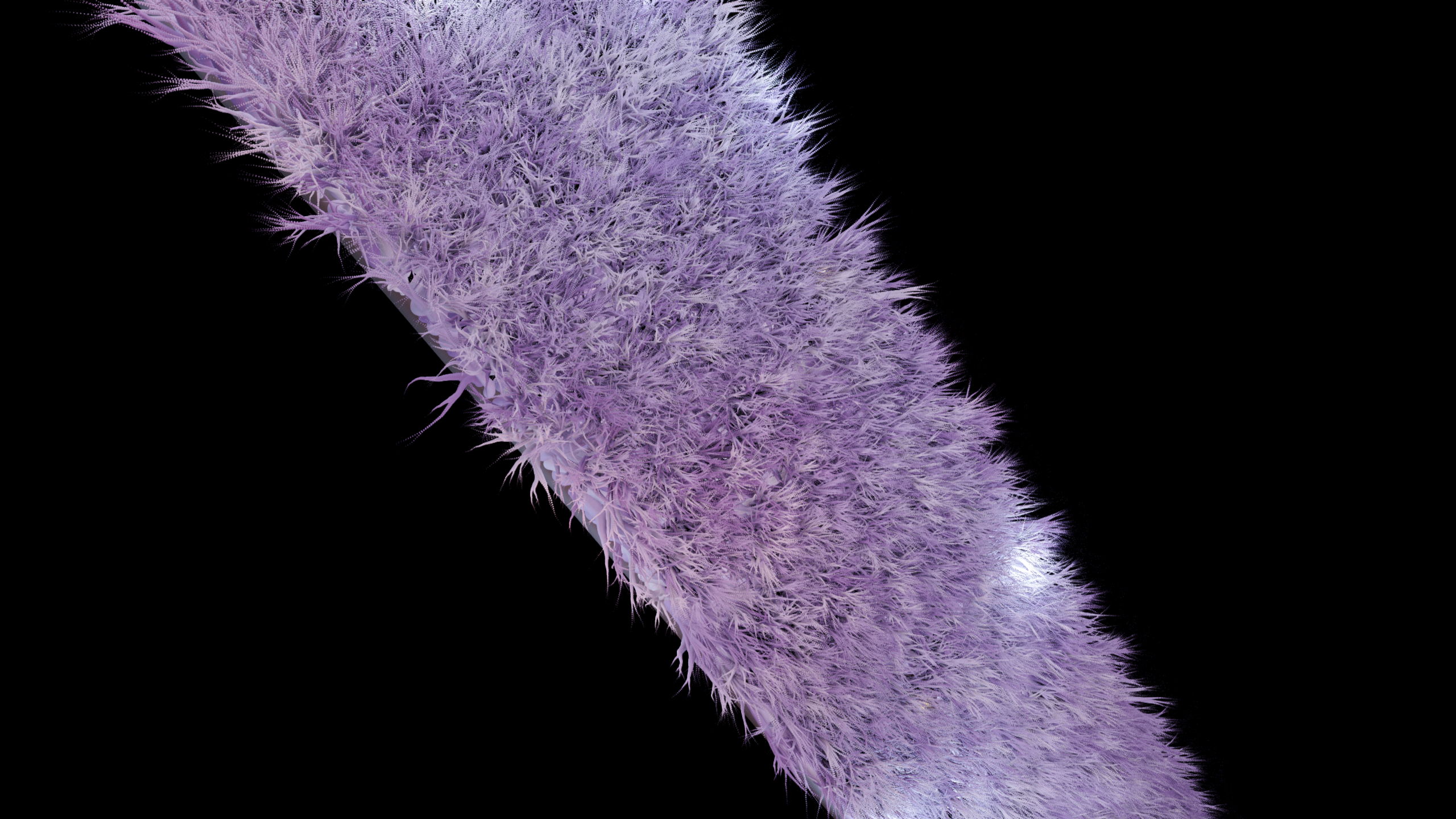
I think this is a hell of an effect, for as simple as it is in implementation. There is a lot of potential in this technique, I think. In order to animate these things in realtime, you would have to start looking at something like motion vectors, which inform the TAA as to where the geometry is moving between frames.

Future Directions
I have thought about other ways to use this technique. The pythagorean theorem based method for evaluating the spheres is a simplified raytrace - maybe the simplest case, other than just using the point, raw - there's nothing to keep you from doing other intersection methods, using the point coord's UV to generate the ray origins / directions. Something I had considered - you could do a small raymarch, support arbitrary geometry inside of the point primitive, whatever rotation etc you wanted to consider. The key things you would need are a way to determine a boolean hit / no hit, the depth offset, and the normal. This could easily be supported by raymarching or ray-primitive intersections.
I also was thinking about investigating other screen space effects - things like screenspace depth-based depth of field, bloom, edge detection, and postprocess distortion. Because everything is done in terms of flat textures with a deferred pipeline setup like this, it's very easy to manipulate the texcoords and get nearby samples to implement these kinds of effects.
One other thing I was considering was the use of something like instancing. Because the deferred stuff happens on flat images, you could just write as much geometry as you wanted to the buffer, and you would still basically have a constant cost for evaluating all the lights. And this doesn't all have to happen in one frame - I have a theory that the old windows pipes screensaver used a similar approach - progressively drawing to the Gbuffer, without clearing between frames. Because everything is static, unchanging once drawn, you never have to worry about recalculating anything other than the pixels most recently drawn. Color and depth buffers are easily retained, and each frame's writes are cheap, incremental changes. You could apply similar logic here, and draw potentially billions of points to the buffer, incrementally, and use the hair / fur rendering approach for rendering vast fields of grass. I think it could scale quite well, to produce some very high fidelity effects.
Overall, I am extremely pleased with how this project went. It is leaps and bounds above what I was able to do with it in the previous writeup, and a damn sight from where I was at with it with the initial implementation in the original Vertexture project.