
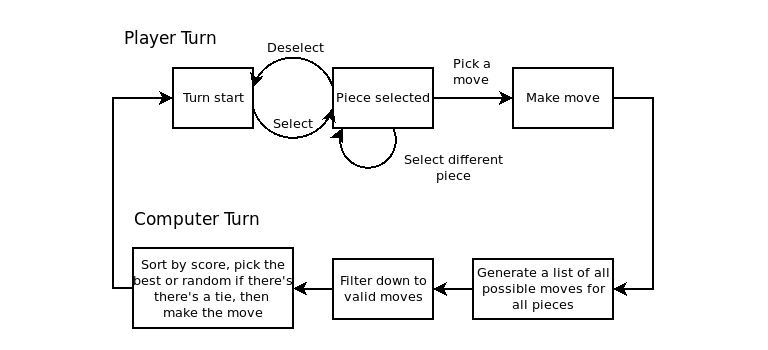
When I was younger, my grandpa made a point to teach me chess very early on. I knew how all the pieces moved and how to play by the time I was 5 years old – I was part of a group that started a chess club in elementary school, and participated in an existing one in middle school. In my CS2400/2401 Intro to C++ classes, we had a multi-part project, the goal of which was to make a checkers program with command line input and output, and implemented some simple AI which would look at a branching structure of all possible moves (plus all possible next moves, and the moves after that, to some defined depth) and count up the number of pieces left in order to make a decision on what move to make. This was initially conceived as a something along those lines, but with OpenGL output. All the graphical elements are finished, and the display reads from the current state of the board in order to know what to draw. I have not finished the game logic but I would like to come back to it and finish it at some point – I have this flowchart drawn up on how to do the rule checking and manipulate the board state but I have not implemented it yet.
This was the first project that I did with OpenGL+SDL2. My first impression was that I liked it a lot more than GLUT, and that I really liked how the events were handled, as it unified most of the different functions that GLUT has callbacks for into one system. I really liked all the system query stuff that’s built in, too. It’s better supported on different linux distros than GLUT – Ubuntu doesn’t come with GLUT at all, you have to install it, but it’s got an up-to-date version of SDL2 included by default. I’ve been using SDL for all the projects I’ve done since, and converted a couple of my GLUT programs to SDL (the SDL event system makes this very easy to do).
REPRESENTATION
The game of chess is relatively simple – you’ve got an 8x8 board, the same as you would use for checkers. There are 16 pieces of each color, eight pawns, two rooks, two bishops, two knights, a queen and a king. There are relatively classical shapes for each of these pieces, and I wanted to put together a decent representation of these shapes. Most have radial symmetry (with the exception of the knight, the bishop, the king, and to a lesser extent the rook), which led me to think about some sort of rotational method to generate this geometry. My thinking was inspired by the idea of a lathe, if you define a profile of this shape, as a series of points in an XY plane, you can rotate by steps around the Y axis to generate these radially symmetric shapes. I found a picture of all the chess pieces, overlaid a grid, and picked points which would define this profile. For my purposes, all pieces share a base, so the points to generate the geometry for the lower section is common to all pieces. As I mentioned before, there are a few less-than-perfect candidates for generating geometry this way, but for the purposes of this project I did not get into correcting it (the slot in the top of the bishop, the horse head on the knight, the crenelations on the top of the rook, the cross on top of the king).

As you do this rotational operation, each step, you look at the points from the previous incremental rotation and the current incremental rotation, and stitch them up using quads. I also computed normals here by using the cross product of the two sides of each triangle involved. The board is represented as black and white squares, just quads, with a bit of a beveled edge around it.
GAMEPLAY
When the game starts, all the pieces are put in their initial positions – the home row goes rook, knight, bishop, queen, king, bishop, knight, rook – the ordering of king and queen vary by which side you are on – the rule is, ‘queen is on her color’. The row in front of that is just eight pawns.

I have a selection scheme implemented as well – in the same way that Vertexture used the red and green color channels to represent the X and Y positions, this game implemented a very similar approach. However, because the user might want to click on the piece, and not just the board square that a piece sits on, each the color of each board square extends to the piece which sits on the square. Again, this is all rendered in a back buffer, the color is picked, then this display is cleared and the regular board is redrawn, so the user never sees this red and green representation during normal gameplay.

RENDERING
In order to reduce the amount of geometry being held, I have only one set of geometry for each piece type - this is just points and normals. When they are drawn, there are uniform values passed in that tells where it is to be drawn (an offset in the board’s plane), a color, a selection color and a mode. The color is used as a base color when applying the Phong shading, and represents which side the piece is associated with. The selection color is somewhat redundant since you have the offset and the shader could compute these things, but for simplicity’s sake, I’m just passing in selection color values so I know exactly what to expect out for each piece or board square. The mode is just a bool that tells whether to render with phong shading or flat shading with the selection color.

The two most interesting parts of this project, I think, are the selection scheme and the driver behavior that I found. I encountered it entirely by accident, an interesting bit of driver behavior that gave some really very visually cool results. The undefined behavior of using an uninitialized variable in a shader is implementation specific, and on the version of Mesa that I was running on my laptop, uninitialized variables used in place of the vertex normals took on random values which gave this very impressive looking effect that almost looked like the pieces were made of glass. I can only speculate, because I don’t have any sense of how they were initialized, what kind of data was used, because it seems pretty clear to me that they were not just zero-initialized (unless maybe this is an effect of dividing by zero somewhere?). In the animation above, I've included recordings taken with two different versions of Mesa - the behavior seems to vary quite a lot by the version you use.